Data analytics for insurance loss modelling, telematics pricing and claims reserving.

In the insurance sector, data have always played a major role. When selling a contract to a client, the insurance company is liable for the claims arising from this contract and will hold capital aside to meet these future liabilities. As such, the insurance premium has to be paid before the real costs are known. This is referred to as the inversion of the production cycle. It implies that the activities of pricing and reserving are strongly interconnected in actuarial practice. On the one hand, pricing actuaries have to determine a fair price for the insurance products they want to sell. Setting the premium levels charged to the insureds is done in a data driven way where statistical models are essential. Risk-based pricing is crucial in a competitive and well-functioning insurance market. On the other hand, an insurance company must safeguard its solvency and reserve capital to fulfill outstanding liabilities. Reserving actuaries thus must predict, with maximum accuracy, the total amount needed to pay claims that the insurer has legally committed himself to cover for. These reserves form the main item on the liability side of the balance sheet of the insurance company and therefore have an important economic impact.

The ambition of this research is the development of new, accurate predictive models for the insurance work field. The overall objective is to improve actuarial practices for pricing and reserving by using sound and flexible statistical methods shaped for the actuarial data at hand. This thesis focusses on three related research avenues in the domain of non-life insurance: (1) flexible univariate and multivariate loss modeling in the presence of censoring and truncation, (2) car insurance pricing using telematics data and (3) claims reserving using micro-level data.

After an introductory chapter, we study mixtures of Erlang distributions with a common scale parameter in Chapter 2. These distributions form a very versatile, yet analytically tractable, class of distributions making them suitable for loss modeling purposes. We develop a parameter estimation procedure using the EM algorithm that is able to fit a mixture of Erlang distributions under censoring and truncation, which is omnipresent in an actuarial context.

Chapter 3 extends the estimation procedure to multivariate mixtures of Erlang distributions. This multivariate distribution generalizes the univariate mixture of Erlang distributions while preserving its flexibility and analytical tractability. When modeling multivariate insurance losses or dependent risks from different portfolios or lines of business, the inherent shape versatility of multivariate mixtures of Erlangs allows one to adequately capture both the marginals and the dependence structure. Moreover, its desirable analytical properties are particularly convenient in a wide variety of insurance related modelling situations.

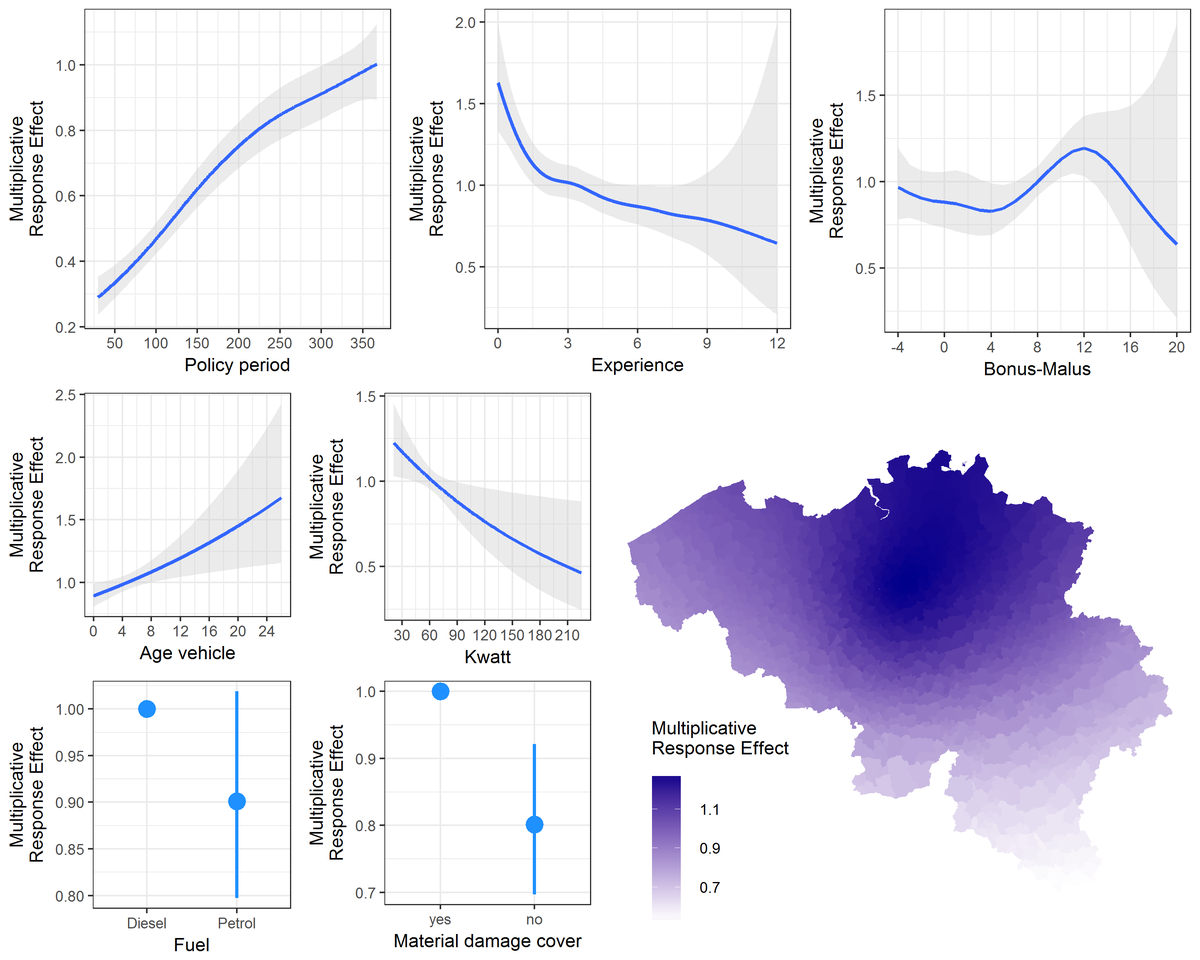
In Chapter 4 we explore the vast potential of telematics insurance from a statistical point of view. We analyze a unique Belgian portfolio of young drivers who signed up for a telematics product. Through telematics technology driving behavior data are collected in between 2010 and 2014 on when, where and how long the insured car is being used. The aim of our contribution is to develop the statistical methodology to incorporate this telematics information in statistical rating models, where we focus on predicting the number of claims, in order to adequately set premium levels based on individual policyholder’s driving habits.

Chapter 5 presents a new technique to predict the number of incurred but not reported claim counts. Due to time delays between the occurrence of the insured event and the notification of the claim to the insurer, not all of the claims that occurred in the past have been observed when the reserve needs to be calculated. We propose a flexible regression framework to model and jointly estimate the occurrence and reporting of claims on a daily basis. The last chapter concludes our work by presenting several suggestions for future research related to topics covered.